Chapter 5.3 Runtime Analysis with Quadratic Speedups

This content of this section corresponds to the Chapter 5.3 of our paper. Please refer to the original paper for more details.

As Theorem 5.1 shows, the quantum transformer uses ${\mathcal{\widetilde{O}}}(d N^2 \alpha_s\alpha_w)$ times the input block encodings, where $\alpha_s$ and $\alpha_w$ are encoding factors that significantly influence the overall complexity. We obtain this final complexity on the basis of the following considerations: for one-single layer transformer architecture, it includes one self-attention, one feed-forward network, and two residual connection with layer normalization, corresponding to the encoder-only or decoder-only structure. Starting from the input assumption, for the index $j\in [\ell]$, we first construct the block encoding of self-attention matrix. This output can be directly the input of the quantum residual connection and layer normalization, which output is a state encoding. The state encoding can directly be used as the input of the feed-forward network. Finally, we put the output of the feed-fordward network, which is a state encoding, into the residual connection block. This is possible by noticing that state encoding is a specific kind of the block encoding. Multiplying the query complexity of these computational blocks, one can achieve the result. The detailed analysis of runtime is referred to @guo2024quantumlinear2024

By analyzing naive matrix multiplication, the runtime of classical single-layer transformer inference is $\mathcal{O}(\ell d + d^2)$, where $d$ is the embedding dimension and $\ell=2^N$ is the input sequence length.

In this section, we provide a combined analytical and numerical analysis to explore the potential of a quantum speedup in time complexity.

Recall that the encoding factor $\alpha$ is lower bounded by the spectral norm of a block-encoded matrix $A$, i.e., $\alpha \geq \left|A\right|$. Given access to quantum Random Access Memory (QRAM) and a quantum data structure [@lloyd2014quantum; @kerenidisQuantumRecommendationSystems2016], there are well-known implementations enable the construction of a block encoding for an arbitrary matrix $A$ where the encoding factor is upper bounded by the Frobenius norm $\left|A\right|_F$. We numerically study these two norms of the input matrices of several open-source large language models[^1].

We first investigate the input sequence matrix $S$, which introduces the dependency on $\ell$. We consider input data in real-world applications sampled from the widely-used Massive Multitask Language Understanding (MMLU) dataset [@hendry2021measuring] covering 57 subjects across science, technology, engineering, mathematics, the humanities, the social sciences, and more. The scaling of the spectral norm and Frobenius norm of $S$ on the MMLU dataset is demonstrated in Figure 5.3. We can find that the matrix norms of the input matrix of all LLMs scale at most as $\mathcal{O}(\sqrt{\ell})$.

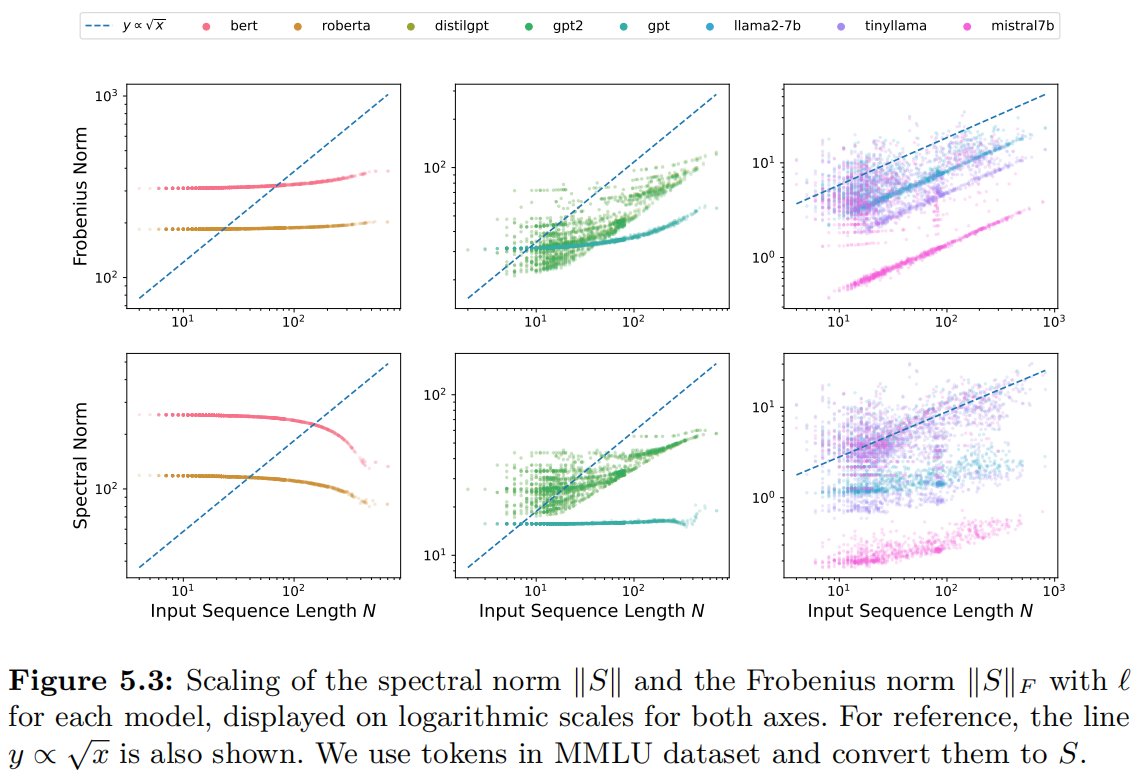
As additional interest, this analysis of the matrix norm provides new insights for the classical tokenization and embedding design. We also observe that comparatively more advanced LLM models like Llama2-7b and Mistral-7b have large variances of matrix norms. This phenomenon is arguably the consequence of the training in those models; the embeddings that frequently appear in the real-world dataset are actively updated at the pre-training stage, and therefore, are more broadly distributed.

We then compute the spectral and Frobenius norms of weight matrices ($W_q,W_k,W_v$) for the large language models. The result can be seen in Figure 5.4. Many of the LLMs below a dimension $d$ of $10^3$ that we have checked have substantially different norms. We observe that for larger models such as Llama2-7b and Mistral-7b, which are close to the current state-of-the-art open-source models, the norms do not change dramatically. Therefore, it is reasonable to assume that the spectral norm and the Frobenius norm of the weight matrices are at most $\mathcal{O}(\sqrt{d})$ for advanced LLMs.

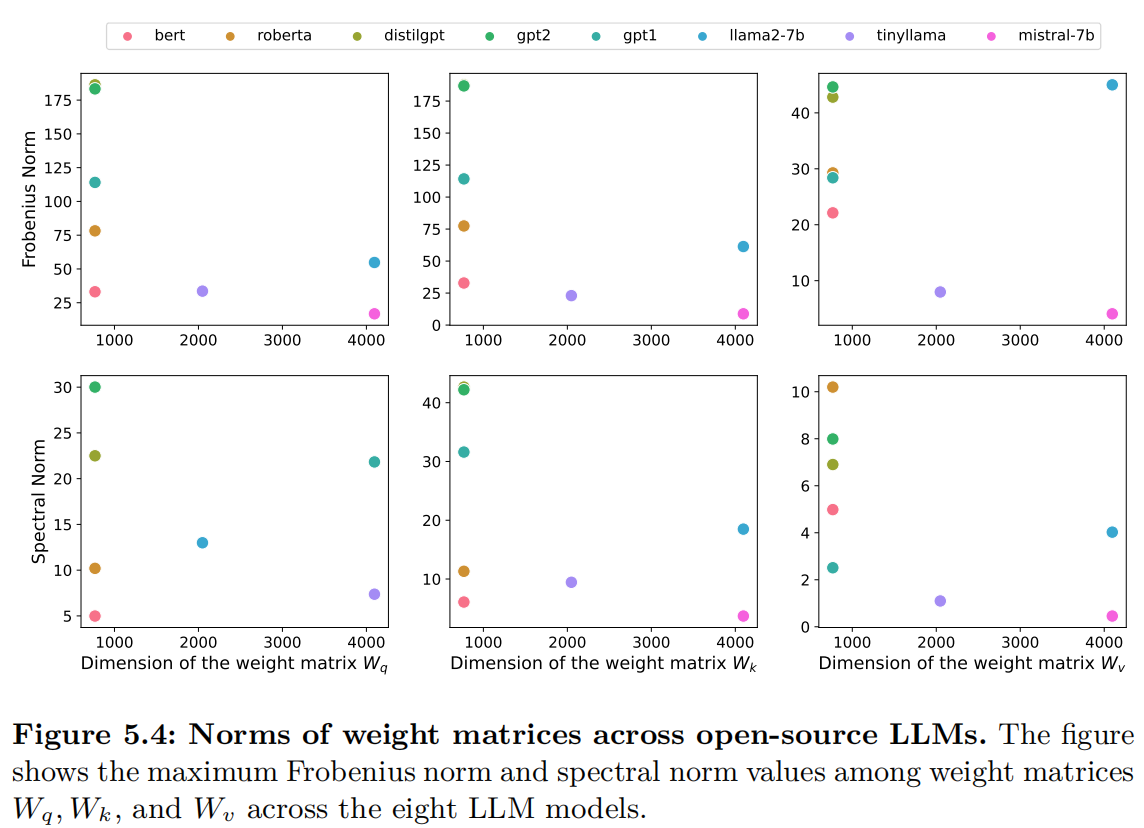
Given these numerical experiments it is reasonable to assume that $\alpha_s = \mathcal{O}(\sqrt{\ell})$ and $\alpha_w = \mathcal{O}(\sqrt{d})$, and we obtain a query complexity of the quantum transformer in $\widetilde{\mathcal{O}}(d^{\frac{3}{2}} \sqrt{\ell})$. We continue with a discussion of the possible time complexity. With the QRAM assumption, the input block encodings can be implemented in polylog time of $\ell$. Even without a QRAM assumption there can be cases when the input sequence is generated efficiently, for example when the sequence is generated from a differential equation, see additional discussions in the supplementary material. In these cases, we demonstrate that a quadratic speedup of the runtime of a single-layer transformer can be expected.